4.4DH参数

DH参数全称为Denavit and Hartenberg Parameter，是指由Denavit和Hartenberg提出的，用于描述机器人（特别是机械臂）的姿态的参数。

具体来说，这些参数描述了机械臂各连杆之间的关系。下面以典型的多连杆机构，来讲述DH参数是如何定义的。

PPT

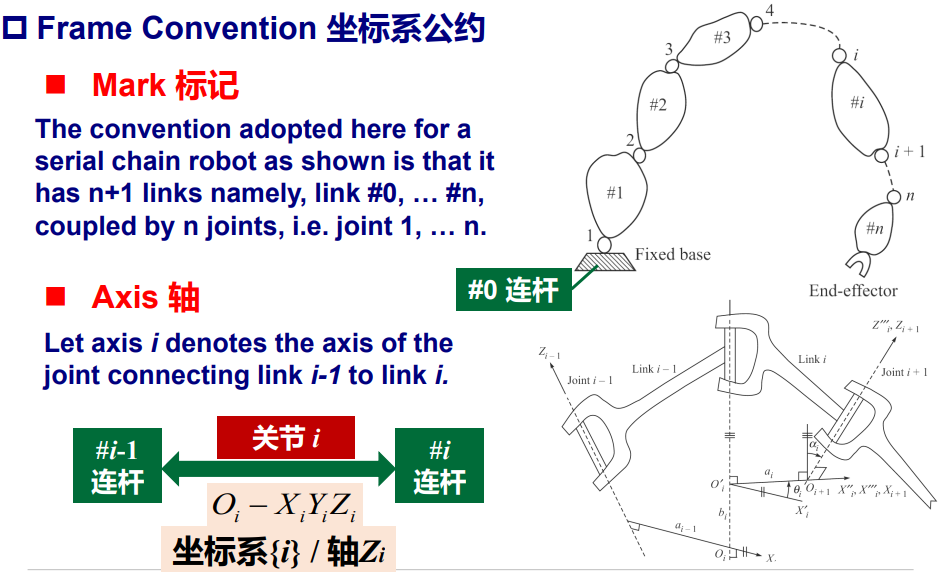
规定固定基座为连杆#0，与基座相连接的关节记作关节1，与关节1相连的下一个连杆记作连杆#2，以此类推。

显然，若有一关节记号为i，则该关节连接了连杆#i-1和连杆#i。

当机械臂中某部分绕着关节i旋转时，为了能使用数学语言描述其旋转前后的姿态，显然，我们需要一个矩阵，这个变换矩阵是一个关于关节i的旋转矩阵（假设其为旋转关节。对于其他类型关节，这样的描述也是相通的），那么，我们就需要一个坐标系，在这里例子中，这个坐标系的某一个轴显然通过该关节的轴。

机械臂上各坐标系的定义

对于任意一种关节，我们采用如下的定义来描述关于这个关节运动过程中的坐标系：

1. 坐标系的\(Z\)轴通过关节的轴
2. 坐标系的\(X\)轴在上一个关节\(Z_{i-1}\)与当前关节坐标系\(Z_i\)的公法线上，且由\(Z_{i-1}\)指向\(Z_{i}\)，\(X\)轴和\(Z\)轴确定后，原点即确定
3. 坐标系的\(Y\)轴由右手坐标系法则确定

此外，还有下列特殊情况：

1. 对于关节1，由于不存在关节0，故其坐标系只有\(Z\)轴是确定的，原点和\(X\)轴可以任意选取
2. 当两个相邻坐标系的\(Z\)轴是平行的，其公法线不是唯一的
3. 当两个相邻坐标系的\(Z\)轴相交，后者的\(X\)轴也是不唯一的

DH参数

对于任意一种关节，Denavit and Hartenberg认为有以下四种参数。对于特定的关节，某几个参数是固定的，称其为连杆参数：

符号	名称	定义
\(b_i\)	关节偏移	\(X_i\)与\(X_{i+1}\)在\(Z_i\)上的距离
\(\theta_i\)	关节角	轴\(X_i\)与\(X_{i+1}\)的夹角
\(a_i\)	连杆长度	轴\(Z_i\)与轴\(Z_{i+1}\)在\(X_{i+1}\)上的距离
\(\alpha_i\)	转角	两\(Z\)轴之间的转角，\(Z_i\)和\(Z_{i+1}\)轴在垂直于\(X_{i+1}\)轴平面上的夹角

对于旋转关节，关节变量(JV,Joint Variable)为\(\theta_i\)；对于移动关节，变量为\(b_i\)。

所讨论的关节i的变量都是对于连杆#i进行的，没有连杆#i，讨论变量就没有意义。

DH坐标变换

对上述讨论的DH参数，我们可以看作如下变换：

1. 先沿着当前坐标系z轴正方向平移\(b_i\)
2. 再沿着当前坐标系z轴旋转\(\theta_i\)
3. 再沿着当前坐标系x轴正方向平移\(a_i\)
4. 最后，沿着当前坐标系x轴旋转\(\alpha_i\)

上述过程中，由于1、2和3、4这两组中两个步骤的分别是关于同一个轴的平移和旋转，所以先后并没有区别，并且可以合并。故对于一个确定了DH参数的机器人的某部位，其坐标变换的齐次矩阵为

\[ T_i = \left( \begin{matrix} \cos \theta_i & - \sin \theta_i & 0 & 0 \\ \sin \theta_i & \cos \theta_i & 0 & 0 \\ 0 & 0 & 1 & b_i \\ 0 & 0 & 0 & 1 \end{matrix} \right) \left(\begin{matrix} 1 & 0 & 0 & a_i \\ 0 & \cos \alpha_i & - \sin \alpha_i & 0 \\ 0 & \sin \alpha_i & \cos \alpha_i & 0 \\ 0 & 0 & 0 & 1\end{matrix}\right) \]

则，对于整个机械臂，其变换为

\[ T = T_1 T_2 T_3 ... T_n \]