AVL树

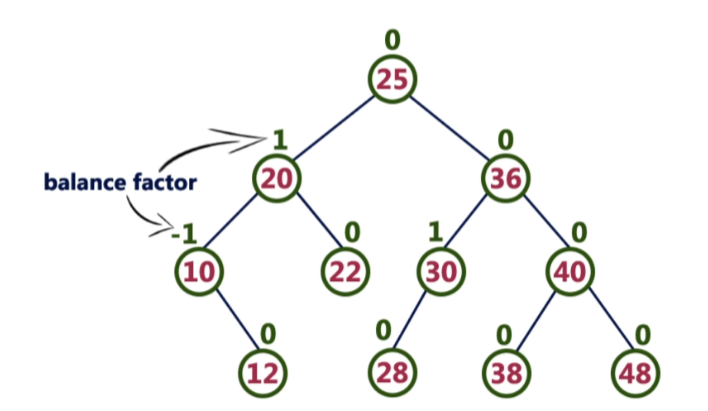
AVL树是一种自平衡二叉查找树。在AVL树中，任一节点对应的两棵子树的最大 高度差 为1，因此它也被称为 高度平衡树 。

AVL树的插入

AVL树的插入可以分成 插入 和 平衡 这两步。

AVL树的插入先是和BST树一样，先插入，但是插入后有可能导致AVL树不平衡，即高度差大于1，此时就需要进行平衡操作，而平衡操作又根据树插入后的状态分为以下三种方式：
1. 左旋 2. 右旋 3. 右旋-左旋 4. 左旋-右旋

所以，AVL树插入后，需要进行上面四种之一的平衡操作，不过在进行平衡操作之前，需要找到最小的和子树，只需要对最小的不平衡子树进行平衡操作即可。寻找最小不平衡子树的方法是从插入出向上查找。

AVL树的平衡方式

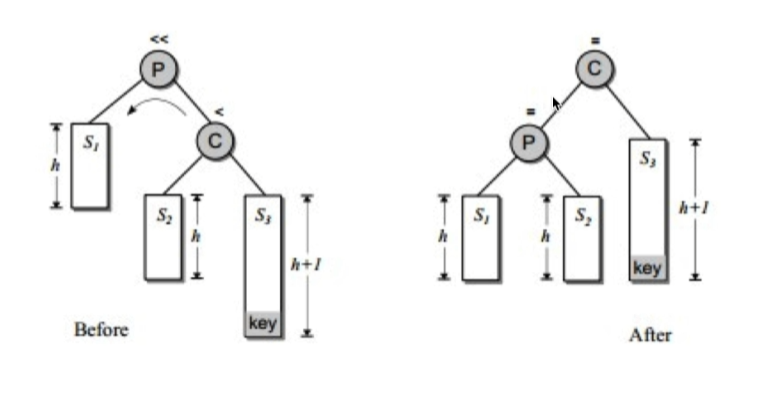
1.左旋

AVL树的不平衡是由于对某节点的右子节点的右子树插入导致的。
左旋的操作如下所示，将右子节点的左子树作为右子节点，将当前节点作为原右子节点的左子节点，原右子节点替代当前节点的位置。

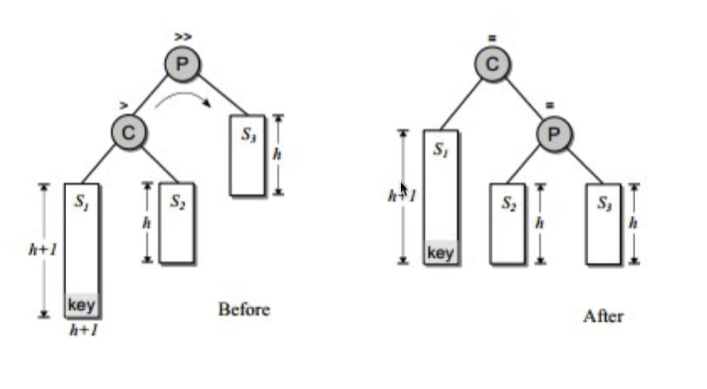
2.右旋

由于对根节点的左节点的左子树插入导致的不平衡。
操作如下：

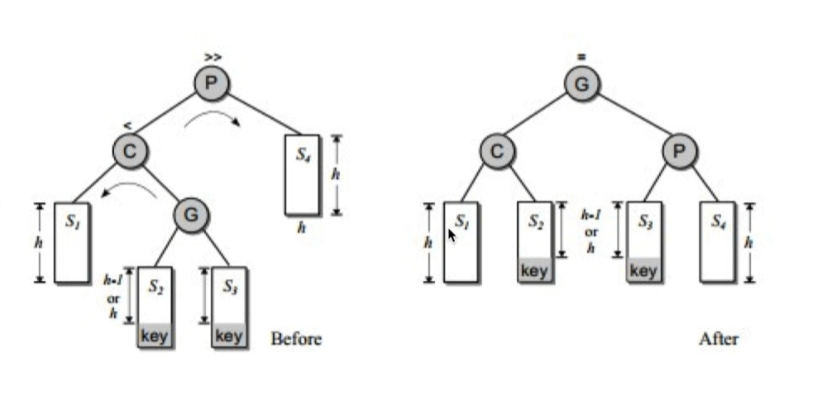
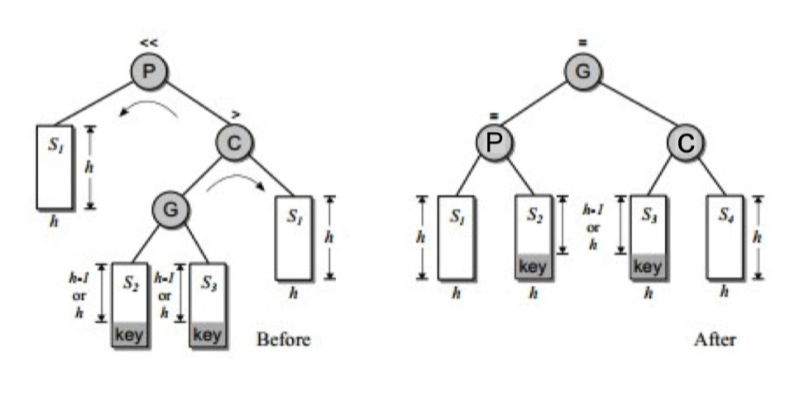
3.右旋-左旋

由于对根节点的右节点的左子树的插入导致的不平衡。
解决方法是先右旋再左旋。

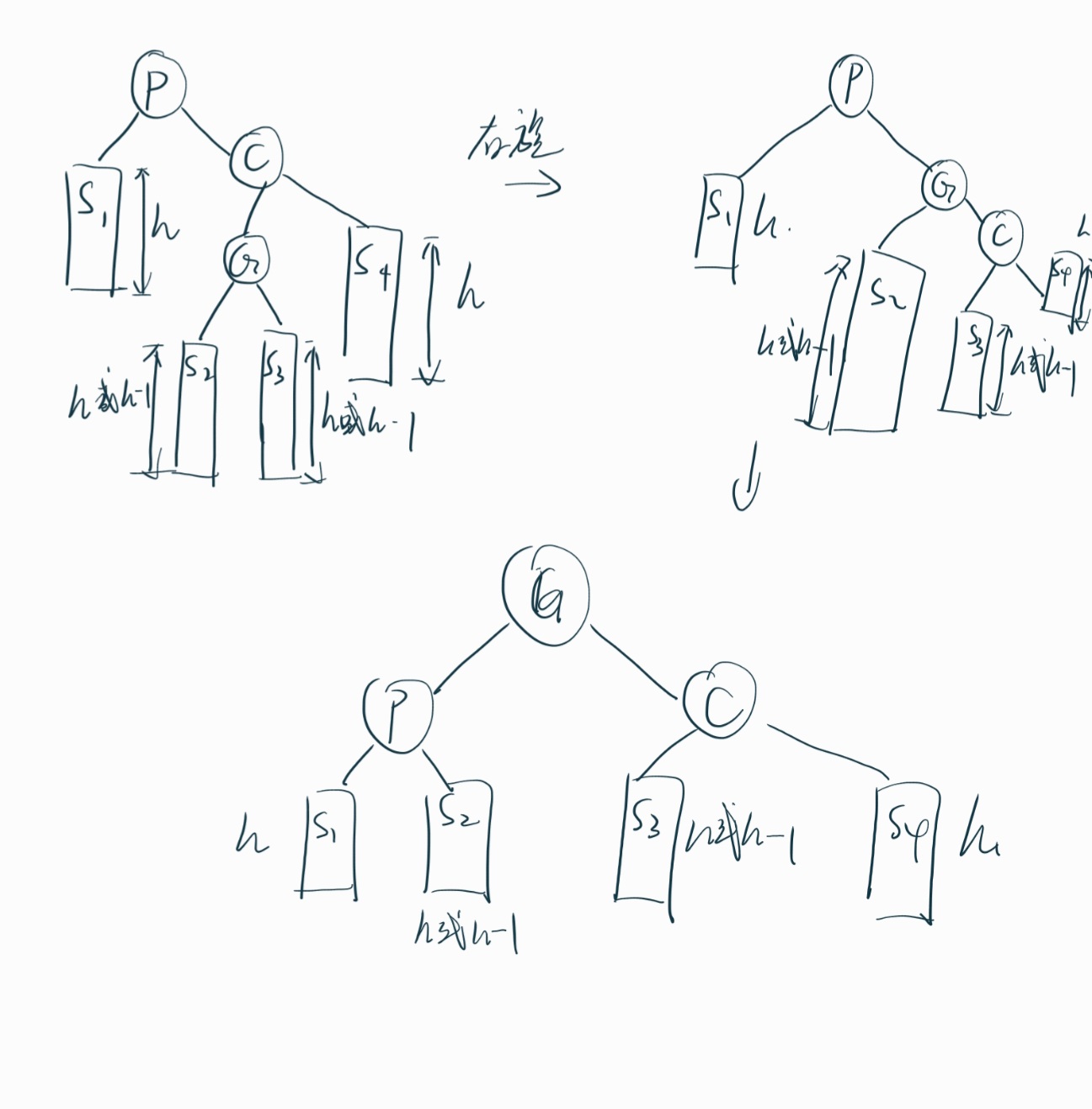
4.左旋-右旋

由于对根节点的左节点的右子树的插入导致的不平衡。
先左旋再右旋。