动态规划 Dynamic Programming¶

动态规划，简称 DP 。

动态规划不是某一种算法，而是一种思想。

动态规划的中心思想¶

递推式
重复的子问题

从斐波那契数列理解动态规划¶

求斐波那契数列中第n项的值可以有以下两种python实现：

def fibonacci_recursion(n):
    if n == 1 or n == 2:
        return 1
    return fibonacci_recursion(n-1) + fibonacci_recursion(n-2)

def fibonacci_no_recursion(n):
    fibonacci = [0 , 1 , 1]
    if n > 2:
        while len(fibonacci) <= n:
            length_fibonacci = len(fibonacci)
            fibonacci.append(fibonacci[length_fibonacci - 1] + fibonacci[length_fibonacci - 2])
    return fibonacci[n]

其中，递归的实现在n很大时，由于重复的子任务执行次数太多，其效率十分低下。而非递归的实现则避免了这一点。非递归的实现就可以看作是一种动态规划思想。

例题¶

1.钢条切割问题¶

问题描述 ：某公司出售钢条，出售价格与钢条长度之间的关系如下。现有一段长度为n的钢条，求切割方案，使总收益最大化。

长度 $ i $	1	2	3	4	5	6	7	8	9	10
价格 $ p_i $	1	5	8	9	10	17	17	20	24	30

解题思路 ：
考虑长度为n的钢条的所有情况是不现实的。先考虑长度小于等于10的钢条，根据上表，长度小于等于10的钢条售出方案可以分为两种——切割和不切割。若不切割，其价格可以在表中得出，若切割，只需考虑怎么分成两部分就行。理由如下：

$ i $	0	1	2	3	4	5	6	7	8	9	10
$ r[i] $	0	1	5	8	10	13	17	18	22	25	30

从长度为0开始考虑。显然，长度为0的钢条最高只能卖0元。长度为1的钢条无法切割，只能按题目所给表卖1元。

而长度为2的钢条可以分为切割与不切割两种。若切割，分为1和1，而两个1的钢条的最优售出价值以求出，为1元，合计2元。若不切割，则按题目所给表，售出5元。显然5元是最优解。

再考虑长度为3的钢条。分成切割与不切割两种，切割则可分为1和2。长度为1和2的钢条的最优售出方案的价格已经算出，分别为1和5.若不切割，则售出8元，显然8是最优方案。

再来看长度为4的钢条，根据上述方法，切割时，分为1和3、2和2两种，分别售出9和10元，不切割时售出9元，因此切割成2和2是最优解。
以此类推……

至于为什么只看切一次的情况，给出理由如下：例如长度为10时，可分为5和5，而5右可以分成5个1或者2加3。但是，长度为5的钢条的最优解已经给出，是在比较了长度为5的钢条的各种切割方法后给出的。可以论证，若切三次讨论售价能产生比只看两次有更优方案，则三次中某两次的和——长度为 $ a $ 的切割方案必然比相应先前求出的长度为 $ a $ 的最优切割方案还要好，但这是矛盾的，因为长度为0、1、2的方案就是最优解，如果存在上述情况，则会出现比表中0、1、2的最优解还要好的方案。很显然，这是不可能的。

上述内容所讨论的可以概括为 最优子结构 ，即问题的最优解是子问题的最优解的和。

根据上述思路，我们可以发现如下递推式：

$ r_n = \max ( p_n , r_1 + r_{n-1} , r_2 + r_{n-2} , \cdots , r_{n-1} + r_1 ) $

式中， $ p_n $ 表示不切割所获得的收益。 $ r_n $ 表示长度为n的钢条的最优方案的收益。

进一步优化，从结果考虑，最优方案一定是由一个不切割的长度和一个切割的长度组成，如9可以看作2+2+2+3，也可以看作3+6，其中6是还需要切割的，3是不用切割的。由此，我们将递推式简化如下：

\[ r_n = \max_{1 \leq i \leq n} (p_i + r_{n-i}) \]

# python
p = [0 , 1 , 5 , 8 , 9 , 10 , 17 , 17 , 20 , 24 , 30]

def solution(p: list , n: int) -> list:
    subSolve = [
        [0 , []] ,
        [1 , [1]] ,
    ]
    if n > 1:
        # 递推
        while len(subSolve) <= n:
            nextIndex = len(subSolve)
            bestDivision = [0 , []]
            # r_n = \max_{1 \leq i \leq n} (p_i + r_{n-i})
            for i in range(1 , nextIndex + 1):
                if i > 10:
                    break
                nowValue = p[i] + subSolve[nextIndex - i][0]
                if nowValue > bestDivision[0]:
                    bestDivision = [nowValue , [i] + subSolve[nextIndex - i][1]]
            subSolve.append(bestDivision)
    return subSolve[n][0] , subSolve[n][1]

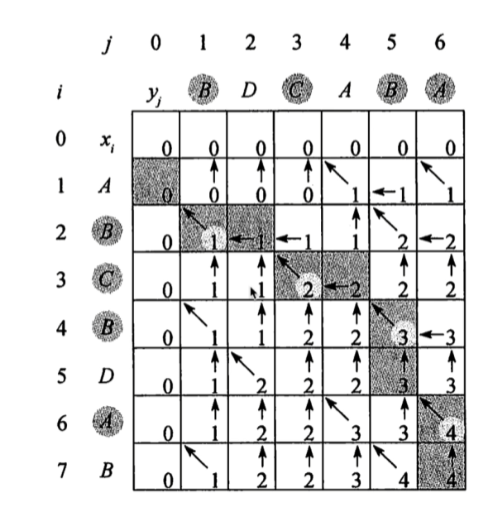
2.最长公共子序列问题¶

现有两个字母序列X和Y，求两个字母串序列的最长公共子序列。
（子序列可以是不连续的，但是顺序不能变）

例如两个序列：
X：ABCBDAB
Y：BDCABA

对于任意两个序列，有以下结论：

若两个序列的尾字母相同，则该字母必然在最长公共子序列Z中；
若两个序列的尾字母不相同，则最长子序列必然是其中一个序列去掉末尾字母后与另一个序列的最长公共子序列。

则有以下的递推式：
$$ c[i , j] = \begin{cases} 0 , (i == 0 ro j == 0) \ c[i-1 , j-1] + 1 , (i,j > 0 and x_i == y_j) \ \max (c[i , j - 1] , c[i - 1 , j]), (i,j > 0 and x_i != y_j) \end{cases} $$

20250223123415

# python
def LCS(x: str , y: str) -> str:
    n = len(x)
    m = len(y)
    res = [[[0 , ''] for j in range(m+1)] for i in range(n+1)]
    for i in range(n+1):
        for j in range(m+1):
            if i == 0 or j == 0:
                continue
            elif x[i-1] == y[j-1]:
                res[i][j] = [res[i-1][j-1][0] + 1 , res[i-1][j-1][1] + x[i-1]]
            else: # x[i-1] != y[j-1]
                if res[i][j-1][0] > res[i-1][j][0]:
                    res[i][j] = res[i][j-1]
                else:
                    res[i][j] = res[i-1][j]
    return res[n][m]