排序(sort)¶
排序是将无序列表排序成有序列表的操作。排序有升序 ascending order 和降序 descending order 之分。
常见排序算法¶
- 冒泡排序 Bubble sort
- 选择排序 Selection sort
- 插入排序 Insertion sort
- 快速排序 Quick sort
- 堆排序
- 归并排序
- 希尔排序
- 计数排序
- 基数排序
1.冒泡排序 bubble sort¶
比较列表中两个相邻数,如果前面比后面大(升序排序),则交换两个数。
冒泡排序每运行一个循环,列表有序区大小变大一个,无序区大小减小一个。每次只对无序区排序。初始时,整个列表都是无序区。
因为当无序区只剩一个时,不用再排序,所以整个冒泡排序需要运行 \( n-1 \) 次循环。时间复杂度为 \( O(n^2) \) 。
冒泡排序的关键: 循环次数 、 无序区范围 。
代码实现¶
# python
def bubble_sort(li: list):
# ascending order
loopTimes = len(li) - 1
for i in range(loopTimes):
for j in range(0 , loopTimes - i):
if li[j] > li[j+1]:
li[j] , li[j+1] = li[j+1] , li[j]
改进¶
若某次循环中,没有发生交换,则说明排序已经完成。可以使用一个变量作为标志位来改进算法。
实现如下:
# python
def bubble_sort(li: list):
# ascending order
loopTimes = len(li) - 1
for i in range(loopTimes):
exchange = False
for j in range(0 , loopTimes - i):
if li[j] > li[j+1]:
exchange = True
li[j] , li[j+1] = li[j+1] , li[j]
if not exchange:
break
2.选择排序 selection sort¶
循环遍历 \( n \) 次列表( \( n \) 为列表规模)。每次寻找无序区的最小值(升序排序),并按照顺序依次与第 \( i \) 个交换( \( i \) 表示第几大的数),并缩小无序区。
代码实现¶
# python
def sort(li: list):
for i in range(len(li) - 1):
minValue = min(li[i:])
minIndex = li.index(minValue , i)
li[i] , li[minIndex] = li[minIndex] , li[i]
3.插入排序 insertion sort¶
排列元素时如同摸扑克牌一样,将有序区不断扩大,将“新摸到的牌”按元素顺序插入到有序区中。需要比较新元素和有序区元素大小,并实现插入操作。
代码实现¶
# python
def insertion_sort(li: list):
# 升序排序
length = len(li)
for i in range(1 , length):
# print(li , i)
# i 代表有序区右侧索引
# 比较
temp = li[i] # 保存要插入的值
for j in range(i - 1 , -2 , -1):
# 反向遍历
# print(j)
if li[j] > temp and j != -1:
# 如果索引为j的元素比索引为i的元素大,则索引为i的元素应该插入在索引为j的元素前,索引为j的元素后移
li[j+1] = li[j]
else:
# 索引为j的元素小于等于索引为i的元素,插入元素应当插入在j+1,不移动元素,将值插入到j+1
li[j+1] = temp
break
4.快速排序¶
类似二分的理念,从无序列表中随机寻找一个元素(一般选取第一个),通过 Partition 操作,将元素放置在其 正确位置 然后对左右两个无序子列表做相似的分割操作。
快速排序的时间复杂度是 \( O(n \log n) \) 。
Partition¶
使用两个元素记录目标列表的左右端元素索引,将用于Partition操作的元素记为“中间元素”,在升序排序时,依次移动右/左索引标记,将右侧小于中间元素的元素放置在左侧,这样右侧就有一个空位;然后将右侧小于中间元素的数放在左侧,循环往复,直到左侧索引大于右侧。
更优的分区算法——Hoare 分区法¶
若将左侧第一个作为选定量,则从右边开始,向左查找,直到找到比选定量小的数。再从左边向右查找,直到找到比选定量大的数。然后检查是否左右指针相遇,若未相遇,则交换两指针所指的值;若相遇则将选定量与该处交换,然后返回左或右索引。
实现如下:(C++)
int partition(int* li , int left , int right)
{
int randint = random(left , right);
// swap
int temp = li[randint];
li[randint] = li[left];
li[left] = temp;
int tempIndex = left;
while(left < right)
{
// 从右侧开始,寻找比归位数小的
while(left < right && li[right] >= temp)
{
right --;
}
while(left < right && li[left] <= temp)
{
left ++;
}
if(left == right)
break;
int a = li[right];
li[right] = li[left];
li[left] = a;
}
// 找到了正确位置
li[tempIndex] = li[left];
li[left] = temp;
return left;
}
代码实现——递归¶
# python
def partition(li: list , left: int , right: int):
pickOut = li[left]
while left < right:
while left < right and li[right] > pickOut:
right -= 1
li[left] = li[right]
while left < right and li[left] < pickOut:
left += 1
li[right] = li[left]
# 左右交换完成,left=right=捡出元素的正确位置
li[left] = pickOut
return left
def quick_sort(li: list , left: int , right: int):
if left < right:
mid = partition(li , left , right)
quick_sort(li , left , mid - 1)
quick_sort(li , mid + 1 , right)
问题 :
1. 使用了递归,消耗资源
2. 若每次partition的操作元素都是最大或者最小的,则每次递归列表无序长度只会减一,会出现所谓 最坏情况 。(解决方法:将partition选取的元素随机化)
5.堆排序 Heap sort¶
时间复杂度 : \( O(n \log n) \)
堆排序的过程¶
- 建立堆(大根堆)
- 得到堆顶元素,为最大元素
- 去掉堆顶元素,将最后一个元素放在堆顶,通过一次向下调整重新使堆有序,获得第二大的元素
- 重复直至堆为空
代码实现¶
# python
def sift(li: list , low: int , high: int):
i = low
j = 2 * i + 1
while j <= high:
if j + 1 <= high and li[j+1] > li[j]:
j = j + 1
if li[j] > li[i]:
li[j] , li[i] = li[i] , li[j]
i = j
j = 2 * i + 1
else:
break
def heap_sort(li: list):
n = len(li)
# 建堆
for i in range((n-2)//2 , -1 , -1):
sift(li , i , n-1)
# 拿出、排序
high = n - 1
# 交换
while high > 0:
li[0] , li[high] = li[high] , li[0]
# 减小无序区大小
high -= 1
sift(li , 0 , high)
堆排序的实际问题——top k 问题¶
问题描述 : 现在有n个数,需要将前k个最大数按从大到小的顺序输出。
6.归并排序 Merge sort¶
归并操作 :若一个列表分成两段有序列表,则将两段有序列表合并成一个有序列表的操作成为归并。
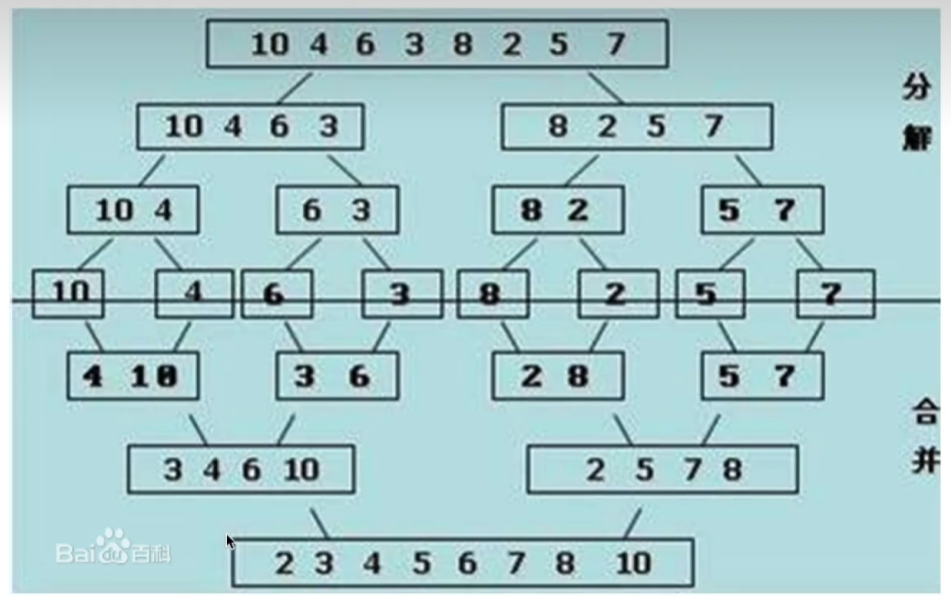
时间复杂度 : \( O(n \log n) \)
代码实现¶
# python
def merge(li: list , low: int , mid: int , high: int):
"""
asceding sort
"""
res = []
i = low
j = mid + 1
while i <= mid and j <= high:
if li[i] > li[j]:
res.append(li[j])
j += 1
else:
res.append(li[i])
i += 1
if i <= mid:
res += li[i:mid+1]
else:
res += li[j:high+1]
li[low:high+1] = res
def merge_sort(li , low , high):
if low < high:
merge_sort(li , low , (low+high)//2)
merge_sort(li , (low+high)//2+1 , high)
merge(li , low , (low+high)//2 , high)
7.希尔排序 Shell sort¶
是插入排序的改进版本,希尔排序通过将比较的全部元素分为几个区域来提升插入排序的性能。这样可以让一个元素可以一次性地朝最终位置前进一大步。
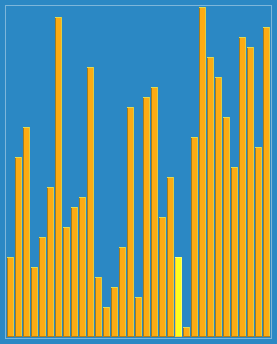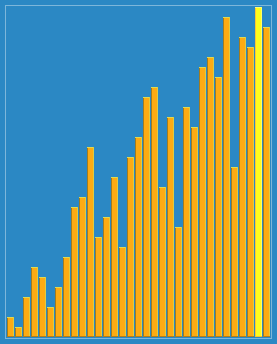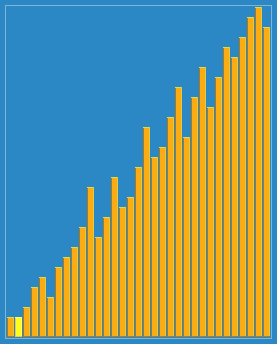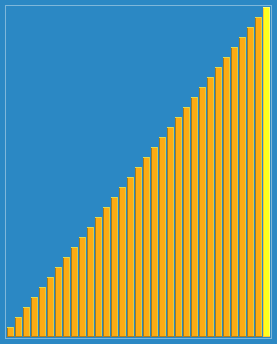
代码实现¶
在插入排序的基础上修改即可,代码如下:
# python
def insertion_sort(li: list , step):
# 升序排序
length = len(li)
for i in range(step , length):
# i 代表有序区右侧索引
# 比较
temp = li[i] # 保存要插入的值
# j = i - step
for j in range(i - step , -2 , -step):
# 反向遍历
# print("j=" , j)
if li[j] > temp and j >= 0:
# 如果索引为j的元素比索引为i的元素大,则索引为i的元素应该插入在索引为j的元素前,索引为j的元素后移
li[j+step] = li[j]
else:
# 索引为j的元素小于等于索引为i的元素,插入元素应当插入在j+1,不移动元素,将值插入到j+1
li[j+step] = temp
# print(f"j={j},break")
break
else:
li[j+step] = temp
def shell_sort(li):
length = len(li)
step = length //2
while step > 0:
insertion_sort(li , step)
step //= 2
8.计数排序¶
任务情景 :现在有一些数,这些数在0到100之间,但数的数量不定,可能超过100,现在需要设计一个时间复杂度为 \( O(n) \) 的算法。
通过建立一个长度为100的列表即可,然后遍历整个数组,记录每个数的出现次数即可,然后输出。
代码实现¶
def count_sort(li , maxCount=100):
count = [0 for i in range(maxCount+1)]
for i in li:
count[i] += 1
# output
index = 0
for i , value in enumerate(count):
while value > 0:
li[index] = i
value -= 1
index += 1
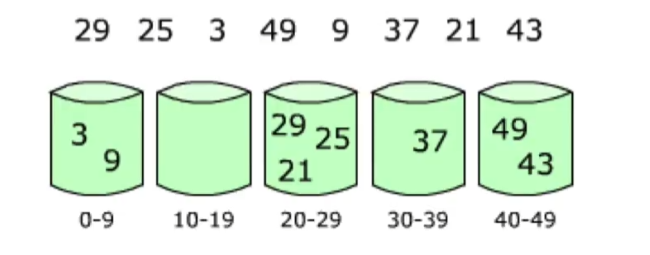
9.桶排序 Bucket sort¶
将元素放在不同的 桶 中,对每个桶进行排序。
桶排序的效率取决于数据的分布,需要采用合适的分桶策略。
代码实现¶
def bucket_sort(li: list , n=100 , maxNumber=100000):
# 创建桶
buckets = [[] for i in range(n)]
# 分桶并排序
for i in li:
targetBucketIndex = max(i//(maxNumber//n) , n - 1)
buckets[targetBucketIndex].append(i)
# bubble sort
for i in range(len(buckets[targetBucketIndex]) - 1 , 0 , -1):
if buckets[targetBucketIndex][i] < buckets[targetBucketIndex][i-1]:
buckets[targetBucketIndex][i] , buckets[targetBucketIndex][i-1] = buckets[targetBucketIndex][i-1] , buckets[targetBucketIndex][i]
else:
break
# 输出
index = 0
for i in buckets:
for j in i:
li[index] = j
index += 1
10.基数排序¶
可以看作多关键字排序。对于数字而言,可以对每一位排序。先对个位排序,然后按顺序输出,再对十位、百位排序。最后输出的就是有序数列。
时间复杂度 : \( O(kn) \)
空间复杂度 : \( O(k+n) \)